流体力学(前編)を読む 第21回
・はじめに
前回は等角写像を簡単にご紹介しました。今回はその本領発揮ということでジューコフスキー変換を学びます。簡単に言うとこれは円柱を平板に写像する関数です。つまり平板に沿って流体が流れたときの様子を知ることができるようになります。そして平板とはほぼ翼のことを指します。なので今回の記事ではいよいよ翼のまわりに生じている流体の動きを細かく見ることができるようになるわけです。そしてとうとう揚力が発生する原理を解明するという当初の疑問にひとまずは一定の解釈を得られることになります。霧がきれいに晴れるような爽快感はありませんが、揚力に関する重要な結論に触れてみましょう。
・本題
として
\begin{equation}
z=\zeta + \frac{a^2}{\zeta} , \hspace{20pt} a>0 \tag{21-1}
\end{equation}
を考える。これをジューコフスキー変換という。論より証拠ということで、まずはfig.1 の通り図示してみた。左が 平面、右が
平面である。

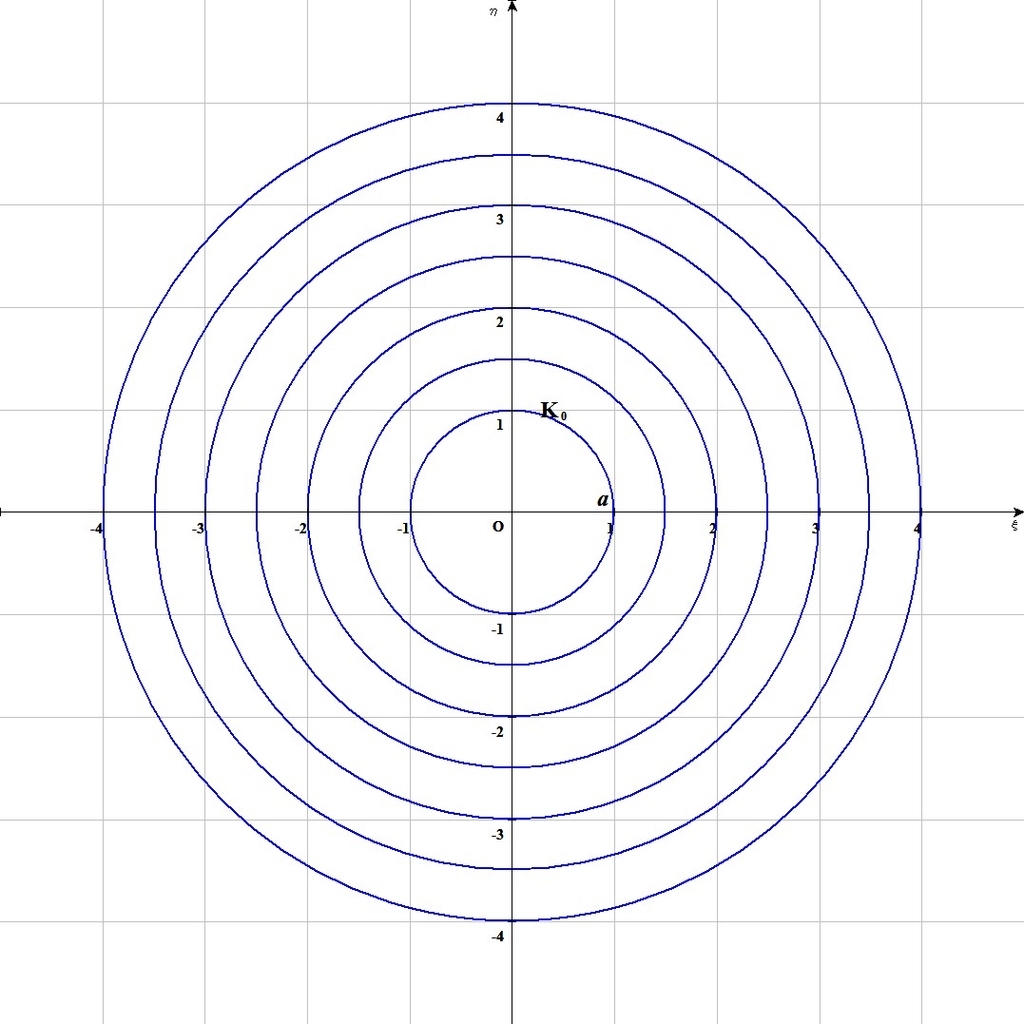
平面には半径
の円を
の値を様々に変化させて描き、これを(21-1)式によって写像させたときの様子が左の
平面に描かれている。これを見るとどうやら円群を楕円群に写像する関数のように思われるが、注目すべきなのは、
平面で描いた半径
の円
が
平面では直径
の線分
に写像されている点である。これが本当に正しいのか、数式を使って検証してみよう。
(21-1)式に対して を代入すると
\begin{equation}
z=Re^{i\theta}+\frac{a^2}{R}e^{-i\theta}=\left( R+\frac{a^2}{R} \right) \cos \theta + i \left( R-\frac{a^2}{R} \right) \sin \theta
\end{equation}
よって実部と虚部で整理すると
\begin{equation}
x=\left( R+\frac{a^2}{R} \right) \cos \theta , \hspace{20pt} y=\left( R-\frac{a^2}{R} \right) \sin \theta
\end{equation}
を得る。これは楕円の方程式の媒介変数表示に他ならず、 としたときには
、
となり確かに円
は線分
に写像されることがわかる。
よってこの写像を用いれば円柱まわりの流れを平板(線分)まわりの流れに変換してその様子を知ることができるようになる。というわけで実際にやってみよう。fig.2およびfig.3に示したのはそれぞれ円柱まわりの流れの様子(左)とそれをジューコフスキー変換によって写像した平板まわりの流れの様子(右)である。ただし一様流は 軸に対して30°だけ傾けている。なぜなら
軸に平行な一様流を当てても平板の場合には流れに変化が得られないからである。
具体的な計算方法はまず円柱まわりの一様流を表す複素速度ポテンシャルの式が
\begin{equation}
f=U(z+\frac{a^2}{z})+i\kappa \log z, \hspace{20pt} \text{a は円柱半径}
\end{equation}
であり、これに前回話した
\begin{equation}
z=g( \zeta)=e^{-i \alpha} \zeta
\end{equation}
を代入することで角度 だけ傾いた流れに写像する。するとfig.2、fig.3の左図を得る。さらに(21-1)式のジューコフスキー変換によって平板まわりの流れに写像すれば右図を得られるというわけだ。ちなみにfig.2は循環なし(
)の流れを表し、fig.3は循環あり(
)の流れを表している。




この平板を平らな翼と見なせば、右図はもはや翼まわりの流れの様子と解釈できる。よってこの流れを詳しく知ることは大変意義深いはずである。そこで例によって複素速度 を求めてみよう。
その前にまず平板まわりに角度 の一様流が流れている場合の複素速度ポテンシャル
を知る必要がある。
は
\begin{equation}
\left\{
\begin{array}{l}
f(\zeta)=U(e^{-i\alpha}\zeta+\frac{a^2e^{i\alpha}}{\zeta})+i\kappa \log \zeta\\[6pt]
z=g(\zeta)=\zeta+\frac{a^2}{\zeta} \tag{21-2}
\end{array}
\right.
\end{equation}
で表現される。第1式は円柱まわりの一様流を角度 だけ回転させるために
に対して
を乗じている。よって第1式からは
平面上に円柱まわりに角度
だけ傾けた一様流が流れる様子が浮かび上がってくる。これはfig.2、fig.3の左図に相当する。そして第2式は今回登場したジューコフスキー変換で 円柱を平板に写像する。よってこれはfig.2、fig.3 の右図に相当する。
では改めて を考えよう。(21-2)式を参考にすると
\begin{equation}
\frac{df}{dz}=\frac{df}{d\zeta} \frac{d\zeta}{dz}=\frac{df/d\zeta}{dz/d\zeta}=\frac{U(e^{-i\alpha}-a^2e^{i\alpha}/\zeta^2)+i\kappa/\zeta}{1-a^2/\zeta^2} \tag{21-3}
\end{equation}
を得る。これは 平面上における流速
を与える式そのものであるが、注目すべきは
では分母が
になり
になることである。
は
に写像されるので、結局平板の両端付近では流速
が無限大に発散してしまうことを意味している。
そしてもちろん流速が無限大というのは現実にそぐわない。ところが平板の先端()では一般に流体の慣性が渦を伴った死水域と呼ばれる空間を形成し流体はなめらかにカーブしながら平板先端を回り込むため有限な速度で流れることができるとされる。しかし平板の後端(
)ではそのような現象が成り立たないようだ。これについては文末の補遺で再度考えてみたい。とにかくここでは平板の後端における流速の無限大のみが問題であるとしよう。そこでこの問題を解消するために
(
) のときに(21-3)式の分子が
になると考える。すると
\begin{eqnarray}
U(e^{-i\alpha}-\frac{a^2e^{i\alpha}}{a^2})+i\ \frac{\kappa}{a}=0\\[6pt]
\kappa=2Ua \sin \alpha \tag{21-4}
\end{eqnarray}
を得る。ここで分子が になるということは当然流速
になるということであり、それはよどみ点のことである。つまりこの場合には
もとい
がよどみ点ということになる。実はfig.3の右図はよどみ点が
(平板後端)に一致するように
を調整したときの流れを描いている。さてここで第15回の記事を思い出すと、渦糸の強さを表す
は静止円柱まわりの一様流について境界条件をもとに計算しても唯一未定の係数であった。だから第16回の記事ではこの
の値を様々に変化させることによって円柱まわりの流れの様子がどう変化するかを観察した。しかし今、この未定の係数であった
は平板の後端付近の流れの不合理を解消したときに一意に定まった。
そして第13回の記事によれば が成り立つから
は循環
を与える。なので平板まわりの流れでは結局循環が一意に定まることになる。さらには循環が定まると今度は第19回の記事で述べたクッタジューコフスキーの定理
\begin{equation}
L=-\rho U \Gamma \tag{21-5}
\end{equation}
により揚力 の値が定まることになるのである。
いま大変重要な結論に至ったので、今度は逆に辿って再度確認しよう。まず揚力 を得るには(21-5)式の通り平板まわりの循環
が要求される。そして循環
は円柱の場合には任意の値を取り得る未知数であったが、平板の場合にはその後端の流速無限大という不合理を解消するために一意に定まった。大まかに言えばこのような論法になる。ここで「平板後端での流速無限大を認めない」という仮定を特にクッタの条件あるいはジューコフスキーの仮定という。しかし仮定というからには所詮仮定である。絶対にこの仮定が正しいと証明できたわけではない。ところが実際の流れにおいても平板の後端によどみ点が存在し、この仮定を満たすような流れになっていることが確認されているようである。
(補遺)平板先端の流速無限大はなぜ許容できるのか
まずは本やネット記事に書いてある主張や解釈を紹介しよう
①流体力学(前編)
本書の章末には次のような説明がある。
物理的には前縁では絶えず境界層が送り出されて停滞するので、いわば渦の帽子をかぶった状態になっている。したがって前縁がよどみ点に一致するということにはならない。いいかえれば、平板は前縁部を丸めた薄翼のようにふるまうのでジューコフスキーの仮定は後縁について考えれば良い。

②二次元翼理論(等角写像とジューコフスキーの仮定)*1
前回から大いに参考にさせていただいているネットの記事である。この中では次のように説明されている。
無限大の速度、無限大の圧力勾配は現実には存在できないので現実の流体は慣性の法則に従って最初の方向を保ったまま流れ去ろうとする。そのために流れは壁から剥離し、渦を伴った死水域が形成される。死水領域が形成されると、流れは滑らかなカープを描いて有限な速度で流れることができる。(中略)前縁では渦の帽子を被ったような状態が実現可能で、前縁を淀み点に一致させなくても前縁を回る流れが無限大速度や無限大速度勾配を必要としない状況を実現できるとする。当然この渦の帽子は揚力の計算値を変化させるはずですが、以後の計算ではその影響を無視しています。
③飛行機はなぜ飛ぶかのかまだ分からない?? 翼の揚力を巡る誤概念と都市伝説*2
こちらの記事も同様に以前から参考にさせていただいている。この中ではどうだろうか。
翼前端で発生した渦は、翼の上面に張り付いて、境界層を作るのである。このように前端と後端の役割が違うのは、実は熱力学第2法則と関係がある。今までの議論で、粘性は関係ないとしていたが、厳密にはそうではなくて、粘性があるからこそ、前後の非対称性が発生するのである。
以上3つの文献を引用した。最後の③で言われているように実際の流体では粘性があり、また境界層があることで流速無限大という不合理が解消されるということらしい。すると要するに今まで前提としてきた完全流体、非粘性、非圧縮などという条件で導かれた理論では、これ以上の解釈は難しいということだろう。
これまでは流体という複雑な現象をいかに単純化してわかりやすく解釈するかという方向で議論してきたが、ここから先は今まで得られた原理原則をいかに拡張して現実に起こる現象を理解していくかという段階に入り、今はちょうどそのターニングポイントに当たると考えられる。よってこの記事も第21回をもってひとつの到達点に達したと考えている。
・まとめ
私は最初、クッタの条件を知ったとき「そんなのあり?」と思ってしまいました。なぜなら(21-3)式が合理的に成り立つための帳尻合わせでしかないと思えたからです。要するに循環が適切な値を持って存在してくれれば、当式の不合理は解消されるということなのですが、結局その循環がなぜ発生するのかというメカニズムについては何も教えてくれなかったわけです。しかしいくつかわかってきたこともあります。
まずひとつめは揚力の要はやはり循環であるということです。少なくとも本書はそのような立場を取っていますし、そこで展開される論理についても概ね理解はできます。
ふたつめは私自身意外でしたが、翼はなにもあの膨らんだ形をしていなくても、たとえば今回のようにただの平板であっても一様流に対して迎え角を持っていれば揚力を発生するという事実です。この点において既に揚力の発生メカニズムを説明する「等時間通過説」*3は誤りであることがわかります。
そしてみっつめは揚力の発生メカニズムをきちんと説明するのは実は極めて難しいということです。参考文献*1の「二次元翼理論(等角写像とジューコフスキーの仮定」の最初の方に翼理論の歴史について書かれていますが、これを読んでいくと揚力の発生原因として循環理論を提唱し、その式として を最初に導いたのはロシアのニコライ・ジューコフスキーという人で1906年の論文に発表されたと書いてあります。一方であまりにも有名なライト兄弟が初めて有人動力飛行に成功したのは1903年です。つまり空を飛ぶということに関しては理論研究よりも実験的な研究の方が先に成功していて、要するになぜかはわからないけどこうすれば飛べるという状況が20世紀初頭の流体力学の実情だったことがわかります。そしてこれを他の物理学の発展と比較すると、循環理論(揚力発生理論)がいかに最近の発見だったかということがわかります。まずニュートンの運動の法則および万有引力の法則発表が1687年、ファラデーの電磁誘導発表が1831年、マックスウェルの電磁場方程式の発表が1861年、プランクの量子仮説発表が1900年、そしてアインシュタインの特殊相対性理論発表が1905年です。いま列挙した物理学の大発見の時系列の中で流体力学は揚力の発生原理を説明することができませんでした。揚力は量子論や相対性理論よりもはるかに身近に感じられ内容は古典力学的でありながらも、その発見はこれら現代物理学とほぼ同時期だったのです。こうして考えるだけでも、いかに翼理論が難しいかということがわかります。このように飛行機が飛ぶというのはもはや身近で一見理屈は簡単そうに思える一方で実際の理論はかなり高度というこのギャップが世の中に誤った理論が溢れる原因ではないかと勝手に想像しています。
以上、長々と書きましたがここまでにわかったことをまとめました。これでもまだ流体力学(前編)の内容でいうと半分も進んでいません。このあとより一般的な厚みのある翼に関する理論があり、2次元から3次元に拡張され、渦理論が導入され、不連続流の話になり、粘性を考慮した流体力学へと理論の幅を広げていきます。私は渦理論あたりで挫折してしまいましたが、そこまで読むだけでも揚力の理論に関してより理解が深まりました。そういうわけで次回以降はちょっと内容が飛び飛びにはなるかもしれませんが、私が面白いと思ったところだけをいくつか取り上げて終わりにしようかなと思っています。
*1:二次元翼理論(等角写像とジューコフスキーの仮定) fnorio.com
*2:飛行機はなぜ飛ぶかのかまだ分からない?? 翼の揚力を巡る誤概念と都市伝説 jein.jp
*3:M理論の部屋 飛行機が飛ぶ理由 飛行機が飛ぶ理由 | M理論の部屋