流体力学（前編）を読む　第８回 - 社会人からの物理と数学

本書　第１８項　渦度と循環

・はじめに
今回からはいよいよ循環を導入します。まずは循環を数学的に定義し、そのあと物理的な意味を解釈していきます。そして後半では循環に関して成り立ついくつかの定理を紹介します。

・本題
循環 $\Gamma$ とは以下の式によって表される
\begin{equation}
\Gamma(C)=\oint_C \boldsymbol{\mathcal{v}}\cdot d\boldsymbol{r} = \oint_C \mathcal{v}_s\ ds \tag{8-1}
\end{equation}
ただし $C$ とは流れの中に取った任意の閉曲線、 $\mathcal{v}_s$ は流速ベクトル $\boldsymbol{\mathcal{v}}$ の $C$ に対する接線成分、 $d\boldsymbol{r}$ は $C$ の線素ベクトルで $ds$ はその長さである。

f:id:youski:20180807150039j:plain:w400

ストークスの定理 *1によれば、この線積分は以下の面積分に変形できる
\begin{equation}
\Gamma(C)=\oint_C \boldsymbol{\mathcal{v}}\cdot d\boldsymbol{r} = \iint_S \mathrm{rot}\ \boldsymbol{\mathcal{v}}\cdot d\boldsymbol{S} = \iint_S \boldsymbol{\omega}\cdot d\boldsymbol{S} \tag{8-2}
\end{equation}
ここで $\boldsymbol{S}$ とは閉曲線 $C$ に囲まれた曲面であり、その方向は法線ベクトル $\boldsymbol{n}$ の向きである。また法線ベクトル $\boldsymbol{n}$ は閉曲線 $C$ の向きが反時計方向に見える面を表としたときに、その表に向かって伸びる向きを指している。
さて（8-2）式が意味するところの循環とは結局、渦度ベクトル $\boldsymbol{\omega}$ が成す渦線が曲面 $S$ をどれだけ貫いているかを表しているに過ぎない。そして曲面 $S$ を貫く渦線群が成すひとつの管を渦管と呼ぶ。

f:id:youski:20180807154917j:plain:w400

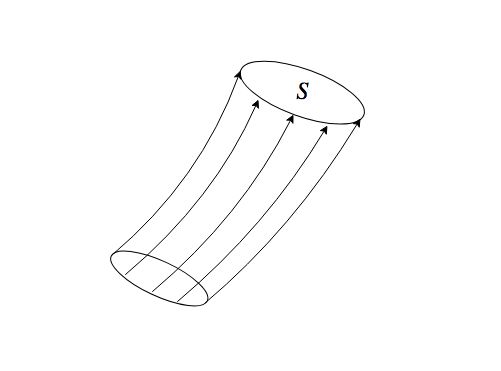
ここで循環と渦についてわかったことを整理しておく。まず循環はある渦管の側面を１周する閉曲線 $C$ について取ると、その $C$ の取り方にはよらず一定である。なぜなら渦管の中にある渦線は勝手に増えたり減ったりはしない（ラグランジュの渦定理）から、それを囲む閉曲線 $C$ 内の渦度の総和はどの閉曲線で取っても常に一定になるからである。またこのことから渦管が流体の内部で途切れることはない。さらに（8-2）式が一定に保たれるということは、渦管の細いところでは渦度が大きくなり、太いところでは渦度が小さくなることもわかる。これはまさに角運動量の保存則と同じ性質であるかのように思われる。

では次にこの循環の性質をもっと知るために、今度は閉曲線 $C$ の時間変化を追って循環が時間的にどう変化するかを考えてみる。たとえば時刻 $\mathcal{t}=0$ に、ある閉曲線 $C_0$ 上にあった流体粒子が時間の経過とともに移動し、時刻 $\mathcal{t}$ に閉曲線 $C$ をつくるものとする。このような変化を知るにはラグランジュ微分を取れば十分である。すなわち
\begin{equation}
\frac{D}{D\mathcal{t}}\Gamma(C)=\frac{D}{D\mathcal{t}}\ \oint_C \boldsymbol{\mathcal{v}}\cdot d\boldsymbol{r}=\oint_C \frac{D}{D\mathcal{t}}(\boldsymbol{\mathcal{v}}\cdot d\boldsymbol{r})\\[12pt]
=\oint_C \left( \frac{D\boldsymbol{\mathcal{v}}}{D\mathcal{t}}\cdot d\boldsymbol{r} + \boldsymbol{\mathcal{v}}\cdot \frac{D}{D\mathcal{v}}d\boldsymbol{r}\right) \tag{8-3}
\end{equation}
が解ければ良い。括弧内の第１項と第２項についてそれぞれ考えてみよう。まず第１項は運動方程式
\begin{equation}
\frac{D\boldsymbol{\mathcal{v}}}{D\mathcal{t}}=\boldsymbol{K}-\frac{1}{\rho}\ \mathrm{grad}\ p = -\mathrm{grad}\ (\Omega + P)
\end{equation}
を代入する。ただしここでは外力が保存力であることとバロトロピー性を仮定している。
第２項は単純に次のように式を整理する
\begin{equation}
\frac{D}{D\mathcal{t}}d\boldsymbol{r} = \frac{D}{D\mathcal{t}} (\boldsymbol{\mathcal{r_2}}-\boldsymbol{\mathcal{r_1}})=\boldsymbol{\mathcal{v_2}}-\boldsymbol{\mathcal{v_1}}=d\boldsymbol{\mathcal{v}}
\end{equation}
ただし $d\boldsymbol{r}=\boldsymbol{r_2}-\boldsymbol{r_1}$ である。これらを代入して（8-3）式を整理すると
\begin{align}
\frac{D}{D\mathcal{t}}\Gamma(C)&=\oint_C \biggl ( -\mathrm{grad}\ (\Omega + P)\cdot d\boldsymbol{r} + \boldsymbol{\mathcal{v}}\cdot d\boldsymbol{\mathcal{v}} \biggl )\\[12pt]
&=\oint_C \biggl( -d(\Omega+P)+d \left( \frac{1}{2}\boldsymbol{\mathcal{v}^2} \right)\biggl)=\oint_C\ d \left( \frac{1}{2}q^2-\Omega-P \right) \\[12pt]
&=\left[ \frac{1}{2}q^2-\Omega-P \right]_C　\tag{8-4}
\end{align}
を得る。ただし最後の式は閉曲線 $C$ を１周したときの変化量を表す。また１行目から２行目の式変形については補遺で解説する。いま括弧内の関数はすべて１価関数であるから、１周しても元に戻れば同じ値になるので結局変化量としては $0$ である。よって結論は
\begin{equation}
\frac{D}{D\mathcal{t}}\Gamma(C)=0
\end{equation}
より
\begin{equation}
\Gamma(C_0)=\Gamma(C)=\mathrm{const}
\end{equation}
となる。結局循環は任意の閉曲線に対して時間的にも一定不変に保たれるのである。これをケルビンの循環定理という。
今までの話から渦管の性質についてまとめると、「渦管は発生したり消滅したりすることなく、渦管のまま移動し、かつその強さは一定不変に保たれる」。このことをヘルムホルツの渦定理という。

（補遺）
\begin{equation}
\mathcal{-}\mathrm{grad} (\Omega + P) \cdot d \boldsymbol{r} + \boldsymbol{\mathcal{v}}\cdot d\boldsymbol{\mathcal{v}} = -d(\Omega+P)+d \left( \frac{1}{2}\boldsymbol{\mathcal{v}^2} \right) \tag{8-5}
\end{equation}
について解説する。この変形を理解するには、全微分の式*2を思い出すとよい。

すなわちあるスカラー量 $\Phi$ の変化量は位置ベクトル $\boldsymbol{r}(r_x,r_y,r_z)$ を用いて以下のように表される
\begin{equation}
d \Phi = \left( \frac{\partial \Phi}{\partial r_x}, \frac{\partial \Phi}{\partial r_y}, \frac{\partial \Phi}{\partial r_z} \right)
\left( \begin{array} {c} dr_x \\ dr_y \\ dr_z \end{array} \right) =( \mathrm{grad}\ \Phi) \cdot d\boldsymbol{r}　\tag{8-6}
\end{equation}
これを用いると（8-5）式の第１項は $\Phi=\Omega+P$ と読み替えれば良い。また第２項は $\boldsymbol{r}$ を $\boldsymbol{\mathcal{v}}$ に、 $\Phi$ を $\displaystyle \frac{1}{2}\boldsymbol{\mathcal{v}^2}$ と読み替えれば
\begin{equation}
d\left(\frac{1}{2}\boldsymbol{\mathcal{v}^2}\right) = \mathrm{grad}\ \left(\frac{1}{2}\boldsymbol{\mathcal{v}^2}\right) \cdot d\boldsymbol{\mathcal{v}}=\boldsymbol{\mathcal{v}}\cdot d\boldsymbol{\mathcal{v}}
\end{equation}
が得られる。