流体力学（前編）を読む　第１６回 - 社会人からの物理と数学

本書　第２８項　静止円柱を過ぎる一様な流れ

・はじめに
　前回に引き続き、円柱を過ぎる流れについて見ていきたいと思います。今回は特に渦糸の強さを表す $\kappa$ の大きさによって流れの様子がどのように変化していくかを図示しながら理解していきたいと思います。

・本題
　まずは円柱を過ぎる一様流が作る流れの一般式を以下に示す。
\begin{equation}
f=Uz+i \kappa \log z +\frac{U}{z} \tag{16-1}
\end{equation}
繰り返しになるが、これは一様流、渦糸、二重わき出しの３つの要素を合成した形となっている。まずはそれぞれの流れの形を以下に図示しよう。
ちなみに図の描画に当たっては function view *1 という関数が描画できる画期的なソフトを使用させていただいた。しかもフリーであるから神である。

f:id:youski:20181005103150p:plain — fig.1

f:id:youski:20181005103202p:plain — fig.1

　次にこれらを合成したときに流れの様子がどうなるか見ていこう。しかしその前に我々は $\kappa$ を決めなければならない。実は $\kappa$ の値によって流れの様子が変わるのだが、それを知るためにまずはこの流れのよどみ点 $z_s$ を調べよう。よどみ点とは流速がゼロになる点なので（16-1）式を微分して複素速度の式に改めそれを０と置けばよいから
\begin{align}
\frac{df}{dz}=U(1+\frac{1}{z_s^2})+\frac{i \kappa}{z_s} &=0\\
z_s^2+\frac{i \kappa}{U}z_s-1&=0\\
z_s=-\frac{i \kappa}{2U} & \pm \sqrt{1-\left(\frac{\kappa}{2U}\right)^2} \tag{16-2}
\end{align}
を得る。この式によれば、 $\kappa < 2U, \kappa=2U, \kappa > 2U$ の３通りの場合を調べれば良いことがわかる。そしてもちろん $\kappa=0$ の場合も考慮する。
　ゆえに場合分けは以下の通りである。

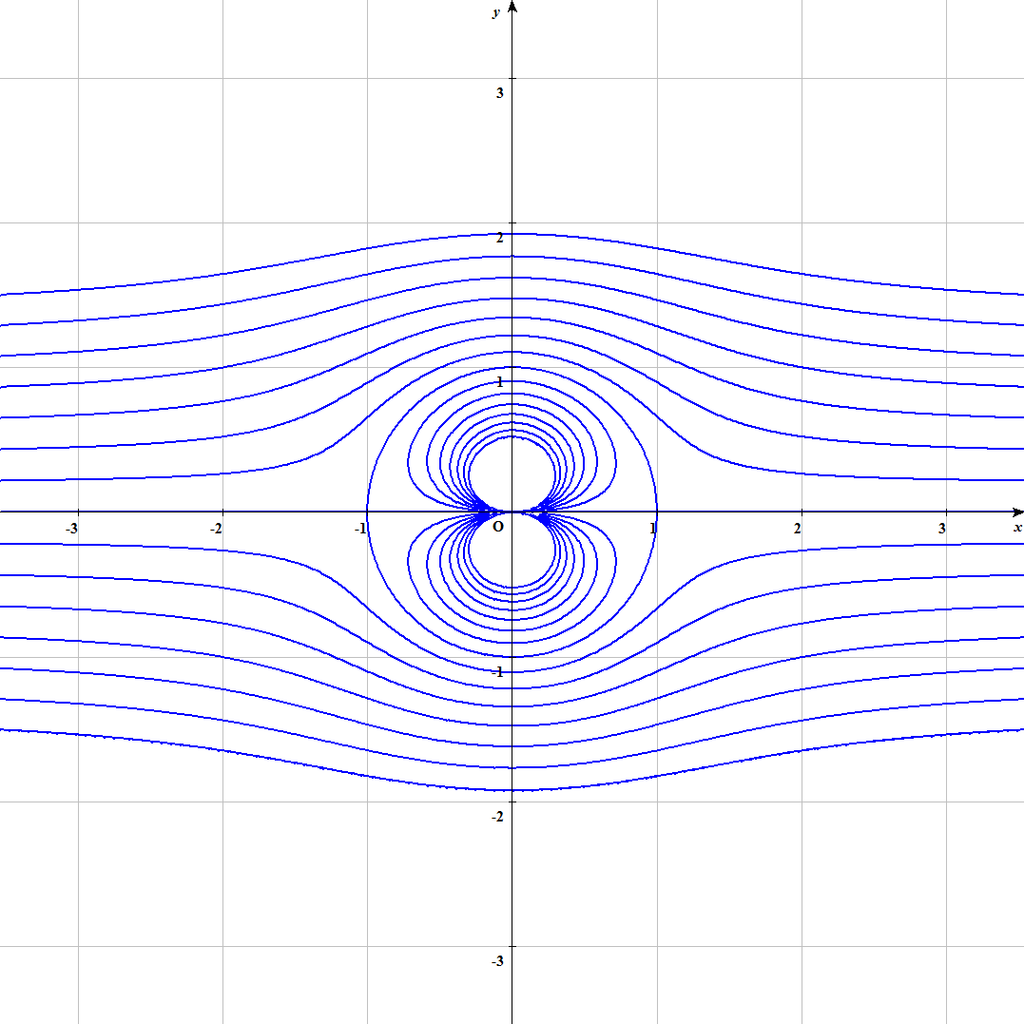
1. 循環がない場合 ( $\kappa=0$ )
　これはただ単に一様流と二重わき出しの合成である。図示すると以下のようになる。

f:id:youski:20181005112523p:plain:w400 — fig.2

おそらく想像通りの流れではないかと思う。しかし二重わき出しをただ置くだけで、そこに円柱があるかのような振る舞いをするというのは興味深い。ちなみに数式的には円柱の内部にも流線を描いているので、円柱を透かして見ると次のような様子が浮かび上がってくる。

f:id:youski:20181005112402p:plain:w400 — fig.3

まるで二重わき出しが一様流によって丸め込まれたような形である。当然円柱内の流線は理論上の線であって実際の流れには存在しない。

2. 循環がある場合 ( $\kappa \neq 0$ )
　それでは今度は先ほどの流れに渦糸を重ねたときの流れを描画してみる。

　2-1. $\kappa<2U$

f:id:youski:20181005113438p:plain:w400 — fig.4

流れがやや下方向に押し出されたような形になった。ここで一様流は左から右へ、渦糸の作る循環は時計方向に向きを持っていたことを断わっておく。これは純粋な渦糸の図からは想像し難い。またよどみ点も円柱下方に移動していることがわかる。興味深いのは循環が存在しても左右の対称性が崩れていない点である。

　2-2. $\kappa=2U$

f:id:youski:20181005113447p:plain:w400 — fig.5

$\kappa$ の値を大きくしたので、流れがより下方向に押し出された。要するに循環とは一様流を曲げる作用を持っていると解釈される。またよどみ点についてはとうとう円柱下端にまで達した。もともと２つあったよどみ点はここで重なり、いわゆる重解となって1点のみになる。

　2-3. $\kappa>2U$

f:id:youski:20181005113452p:plain:w400 — fig.6

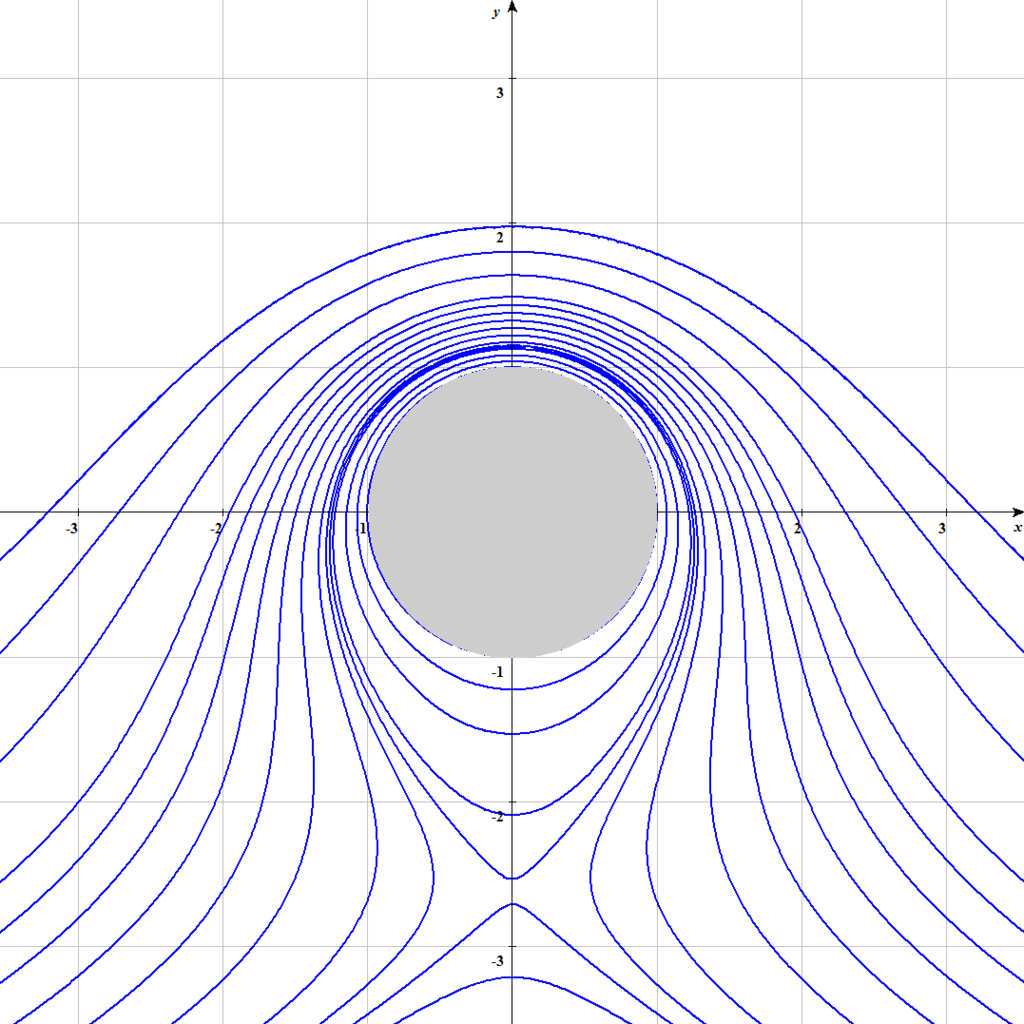
$\kappa$ が 2U を超えるとよどみ点は円柱を離れ虚軸上の負の位置に浮かぶように存在するようになった。またもう一方のよどみ点は理論上は円柱内部に存在するので実際の流れには現れない。

・まとめ
　静止円柱を過ぎる一様な流れについてその一般的な様子をいくつか場合分けをしながらまとめてきました。ですがここでひとつ引っ掛かることがあります。それはなぜ循環が生まれるのかということです。一様流はもともとあったものなので存在に疑問はありません。二重わき出しはちょうど円柱に収まるような形で存在していたので、これが数学的に円柱の役割を果たしていることは容易に想像できます。ところが渦糸はどうでしょう。渦糸がなくても、円柱を過ぎる一様流の様子は十分描けているような気がするし、むしろ渦糸のない流れの方が感覚的には自然です。この渦糸は一体なんなのでしょうか。現時点では答えが見つかりません。ただ実際に流れの様子を描いてみて、この渦糸がどうやら流れの方向を変えているらしいということだけは理解できました。
　またこれに関連して面白いサイトを見つけてしまいました。「鳩ぽっぽ　初心者のための航空力学講座　揚力の発生原理ー飛行機はなぜ空を飛べるのか？」*2です。この記事によると翼が空気の流れを下向きに曲げることで、その押し出した空気の反作用によって揚力が発生するとの説明があります。また空気の流れが曲げられることによって翼の上面と下面に圧力差が生じるという説明がありますが、これは以前第６回の記事で説明した流線曲率の定理にもつながります。つまり渦糸ないし循環による空気の流れへの作用が揚力発生の根本的な原因であることが示唆されます。その循環の発生原理を解明できていないことは大変悔しいですが、とりあえず引き続き本書を読み進めていきたいと思います。次回はベルヌーイの定理を用いて実際に円柱に働く力を求めてみたいと思います。
　

*1:function view functionView

*2:揚力の発生原理ー飛行機はなぜ空を飛べるのか？ pigeon-poppo.com